In the previous lesson, we saw about how to explain fractions. In this lesson, we will see about how to find equivalent fractions.


1/2 is equivalent to 2/4
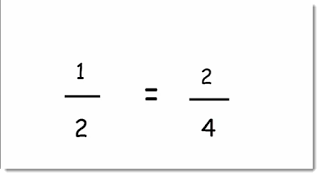
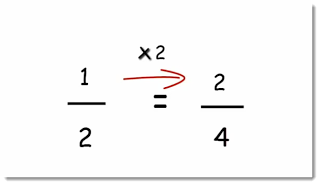
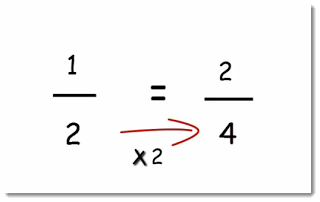


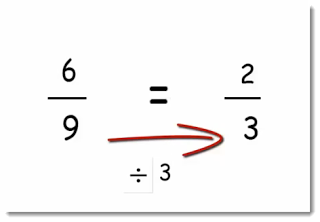
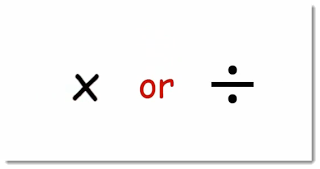
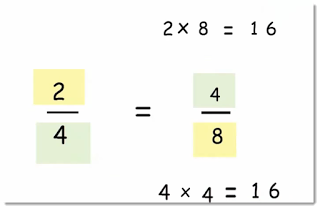
Since both the products are 16, we can say that 2/4 and 4/8 are equivalent fractions.
In math, there are always different ways to arrive at an answer. Let's analyze 2/4 and 4/8 in another way.
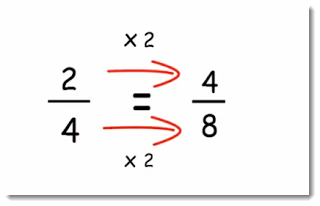

Find the equivalent fraction of 2/4





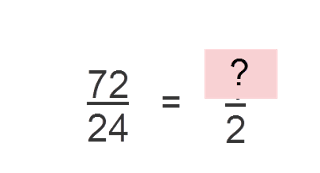
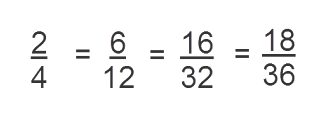
In simple terms, fractions that are similar are known as equivalent fractions. Equivalent fractions when represented pictorially would also look similar.
Examples explain math better than description, so let's see an example.
1/2 is equivalent to 2/4
How can you get 2 from 1? Multiply 1 by 2.
How can you get 4 from 2? Multiply 2 by 2.
So, we multiplied both the numerator and the denominator of one fraction by 2 to get the other fraction.
Another example:
In this example, we divided the numerator and the denominator of one fraction by 3 to get the other fraction.
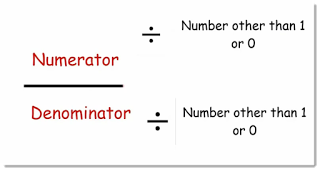
Two fractions are called equivalent fractions when we multiply or divide the numerator and denominator of one fraction by the same number and get the other fraction.
|
You can only multiply or divide to find an equivalent fraction and don't use any other operation such as addition or subtraction.
|
How to find out if two fractions are equivalent fractions?
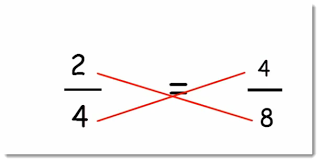
Let's take the fractions 2/4 and 4/8 and find out whether they are equivalent or not.
As shown in the image, we have to multiply the numerator of one fraction with the denominator of the other fraction. This is also known as cross-multiplication. After multiplying, we have to compare the two products. If both the products are equal, then both the fractions are equivalent fractions.
In the above example,
2 x 8 = 16
4 x 4 = 16
Since both the products are 16, we can say that 2/4 and 4/8 are equivalent fractions.
In math, there are always different ways to arrive at an answer. Let's analyze 2/4 and 4/8 in another way.
We can multiply the numerator and denominator of 2/4 with 2 to get 4/8, so we can prove that 2/4 and 4/8 are equivalent fractions.
To find the equivalent fraction of any given fraction, you have to just multiply the numerator and denominator of the given fraction by any whole number other than 1.
Why can't you use 1? What difference is it going to make? Multiplying or dividing a number by 1 is going to give the same number.
Find the equivalent fraction of 2/4
We got 1/2 by dividing both the numerator and denominator of 2/4 by 2.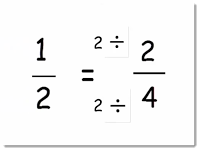
We got 4/8 by multiplying both the numerator and denominator of 2/4 by 2.
So, 1/2 and 4/8 are equivalent fractions of 2/4.
Find the equivalent fraction of 5/7 with numerator 45
To find the answer, let's write the question in a mathematical form.
Simplifying the question is very important in math. Coming back to the question, how many times 5 gives 45?
The answer is 9.
So, multiply the denominator also by 9 to get the answer.
Remember that in equivalent fractions you have to do the same operation (division or multiplication) on both the numerator and denominator.
|
Another example:
Find the equivalent fraction of 81/36 with numerator 9.
On simplifying, we get:
81 divided by 9 = 9
36 divided by 9 = 4
So, 9/4 is the equivalent fraction of 81/36.
Find the equivalent fraction of 72/24 with denominator 2
Remember that when you have to get a smaller number from bigger number you have to use division and when you have to get a bigger number from smaller number you have to use multiplication.
|
If we want to get 2 from 24, we have to divide 24 by 12.
24 divided by 12 = 2
Do the same operation on the numerator also and you would get:
72 divided by 12 = 6
6/2 is the equivalent fraction of 72/24
Before comparing the series of fractions, it would be very helpful if you can arrange the fraction in increasing or decreasing order.
So, the above series can be rearranged as
You can clearly see that 16/32 does not fit in the order, so 16/32 is not an equivalent fraction of the above fractions.
Think what would have happened if I had arranged the series from bigger to smaller fraction.
Thank you for reading this blog! Do mention any suggestions or feedbacks in the comments.
Related Posts: